노이즈 필터

센서 측정과 노이즈

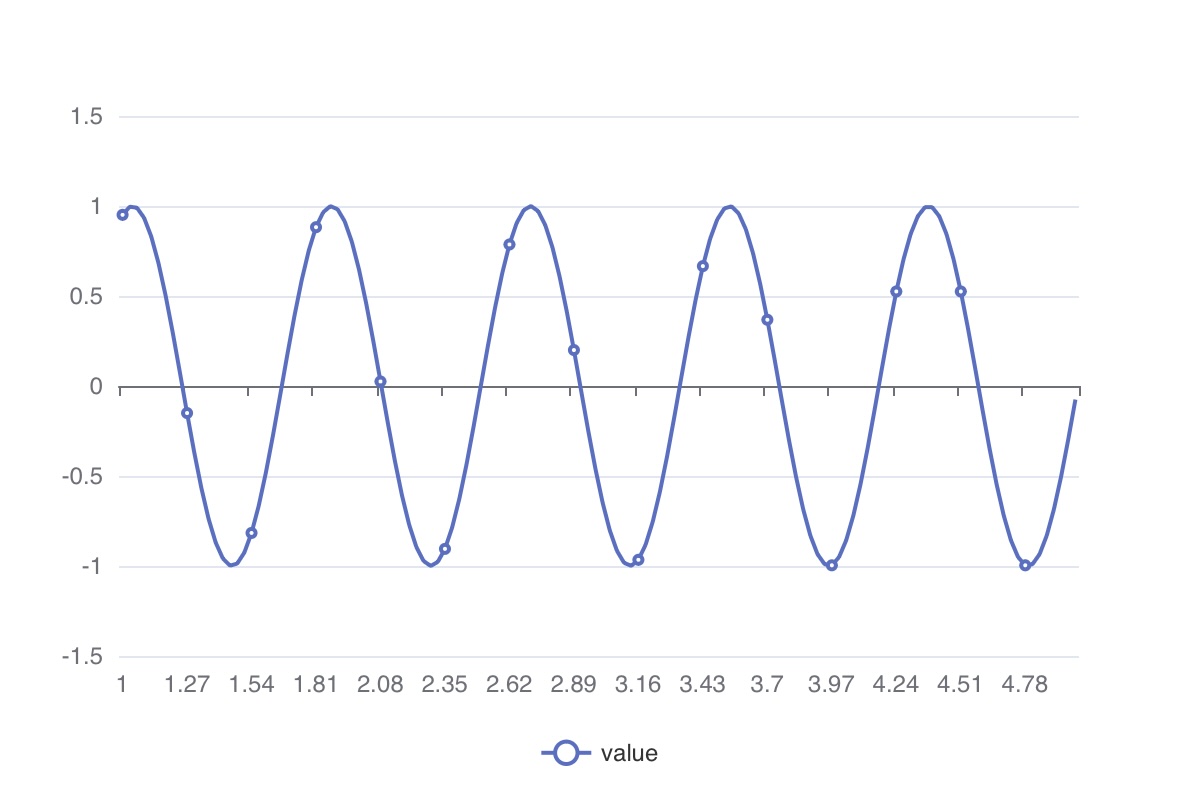
IoT 환경에서 수집되는 값은 모두 센서를 통해 측정된 데이터입니다. 모든 센서는 필연적으로 일정 수준의 노이즈(잡음)를 포함하며, 이론적으로 완전히 깨끗한 데이터는 수학적으로 생성한 가상 데이터일 뿐입니다. 아래 예제는 노이즈가 없는 순수한 신호를 표현합니다.

SCRIPT({
    $.result = { columns: ["val", "sig"], types: ["double", "double"] }
    for (i = 1.0; i <= 5.0; i+=0.03) {
        val = Math.round(i*100)/100;
        sig = Math.sin( 1.2*2*Math.PI*val );
        $.yield( val, sig );
    }
})
CHART(
    size("600px", "400px"),
    chartOption({
        xAxis:{ type: "category", data: column(0)},
        yAxis:{ max:1.5, min:-1.5 },
        series:[
            { type: "line", data: column(1), name:"value" },
        ],
        legend: { bottom: 10 },
    })
)

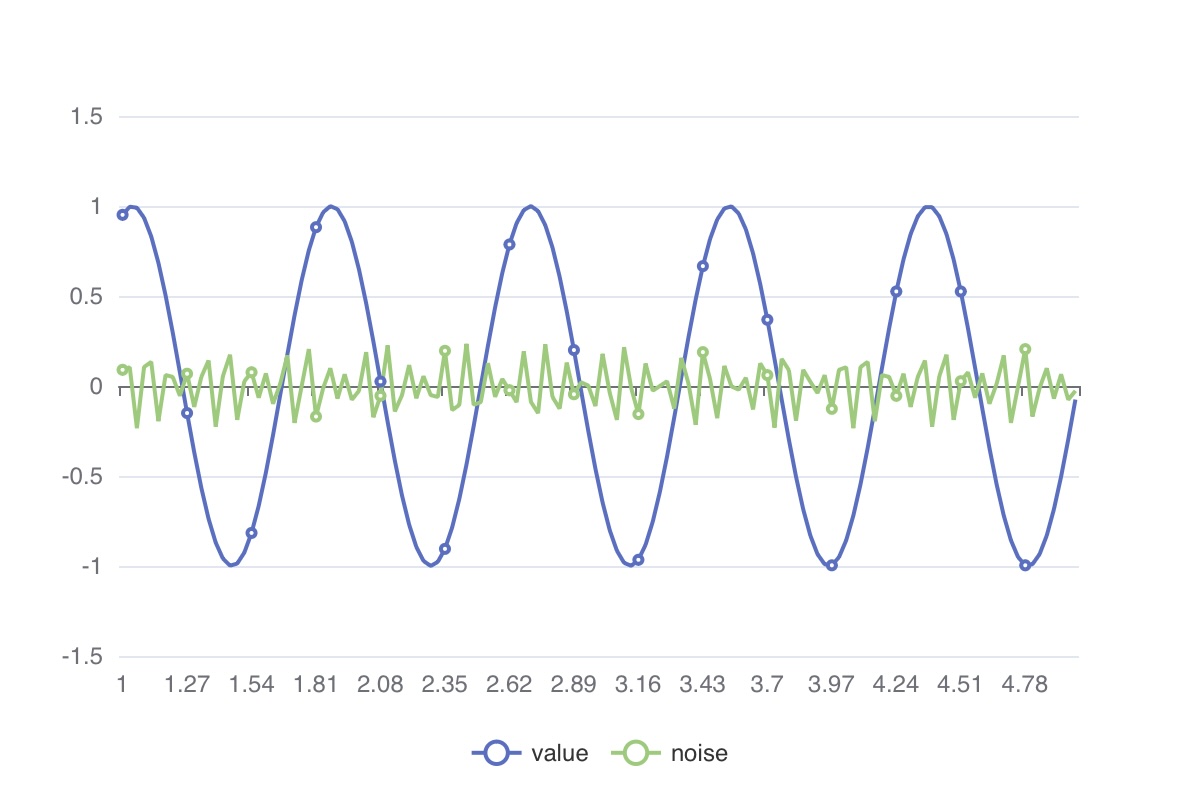
일반적으로 우리가 제거하고 싶은 노이즈는 관측 대상 신호보다 더 높은 주파수를 갖습니다.

SCRIPT({
    $.result = { columns: ["val", "sig", "noise"], types: ["double", "double", "double"] }
    for (i = 1.0; i <= 5.0; i+=0.03) {
        val = Math.round(i*100)/100;
        sig = Math.sin( 1.2*2*Math.PI*val );
        noise = 0.09 * Math.cos(9*2*Math.PI*val) +
                0.15 * Math.sin(12*2*Math.PI*val);
        $.yield( val, sig, noise );
    }
})
CHART(
    size("600px", "400px"),
    chartOption({
        xAxis:{ type: "category", data: column(0)},
        yAxis:{ max:1.5, min:-1.5 },
        series:[
            { type: "line", data: column(1), name:"value" },
            { type: "line", data: column(2), name:"noise" },
        ],
        legend: { bottom: 10 },
    })
)

FAKE(arrange(1,5,0.03))
MAPVALUE(0, round(value(0)*100)/100)

SET(sig, sin(1.2*2*PI*value(0)) )
SET(noise, 0.09*cos(9*2*PI*value(0)) + 0.15*sin(12*2*PI*value(0)))
MAPVALUE(1, $sig)
MAPVALUE(2, $noise)

CHART(
    size("600px", "400px"),
    chartOption({
        xAxis:{ type: "category", data: column(0)},
        yAxis:{ max:1.5, min:-1.5 },
        series:[
            { type: "line", data: column(1), name:"value" },
            { type: "line", data: column(2), name:"noise" },
        ],
        legend: { bottom: 10 }
    })
)

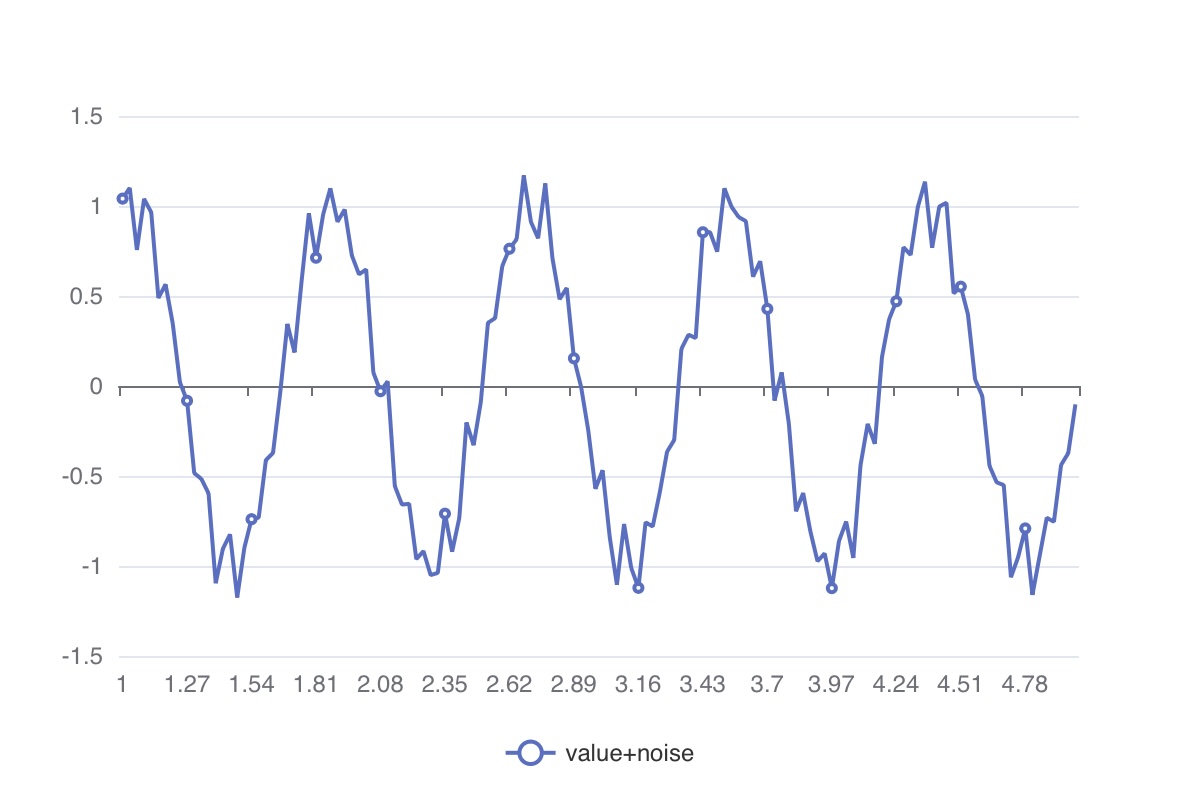
실제 센서로부터 측정된 값은 위와 같은 노이즈가 섞인 형태가 되며, 분석 과정에서는 이 노이즈를 필터링해 신호를 관찰하고 싶어집니다.

SCRIPT({
    $.result = { columns: ["val", "sig"], types: ["double", "double"] }
    for (i = 1.0; i <= 5.0; i+=0.03) {
        val = Math.round(i*100)/100;
        sig = Math.sin( 1.2*2*Math.PI*val );
        noise = 0.09 * Math.cos(9*2*Math.PI*val) +
                0.15 * Math.sin(12*2*Math.PI*val);
        $.yield( val, sig + noise );
    }
})
CHART(
    size("600px", "400px"),
    chartOption({
        xAxis:{ type: "category", data: column(0)},
        yAxis:{ max:1.5, min:-1.5 },
        series:[
            { type: "line", data: column(1), name:"value+noise" },
        ],
        legend: { bottom: 10 },
    })
)

FAKE(arrange(1,5,0.03))
MAPVALUE(0, round(value(0)*100)/100)
SET(sig, sin(1.2*2*PI*value(0)) )
SET(noise, 0.09*cos(9*2*PI*value(0)) + 0.15*sin(12*2*PI*value(0)))
MAPVALUE(1, $sig + $noise)
CHART(
    size("600px", "400px"),
    chartOption({
        xAxis:{ type: "category", data: column(0)},
        yAxis:{ max:1.5, min:-1.5 },
        series:[
            { type: "line", data: column(1), name:"value+noise" },
        ],
        legend: { bottom: 10 }
    })
)

평균 필터

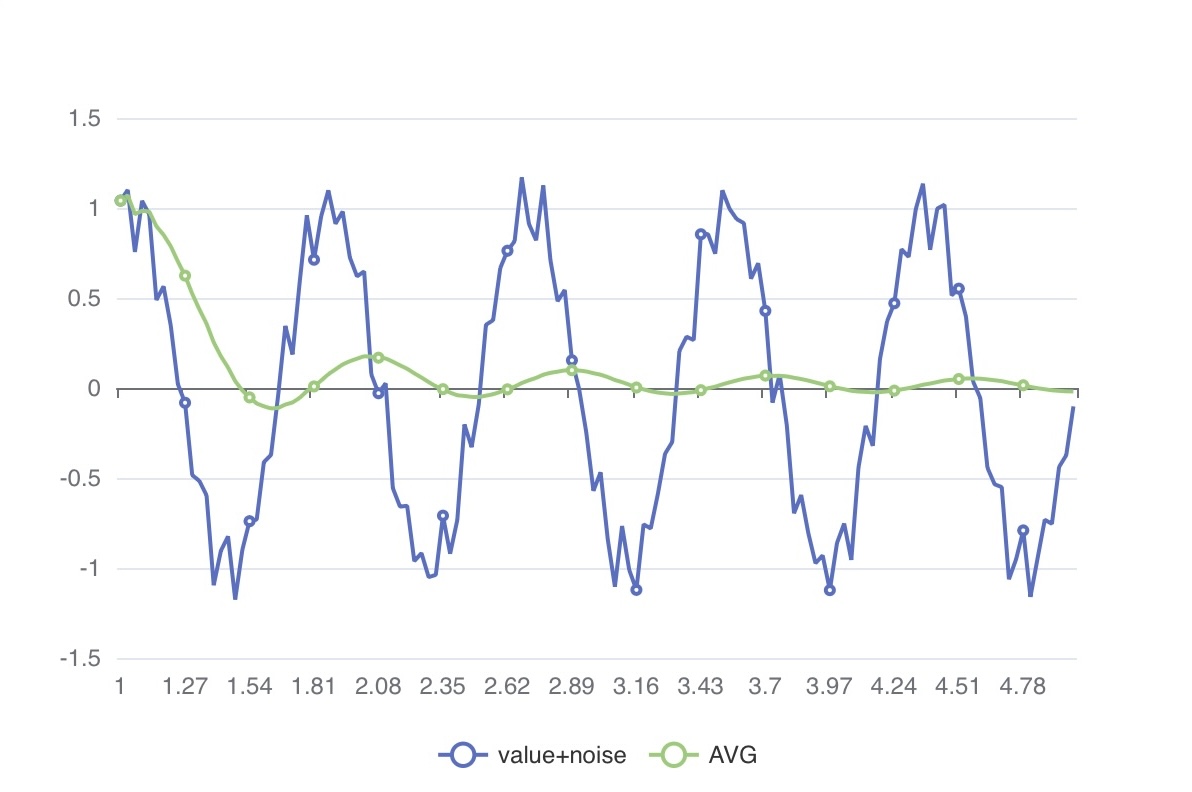
센서의 영점 보정(zero-point calibration)처럼 연속된 값을 평균하면 노이즈가 줄어드는 효과가 있습니다. 아래 예시는 단순 평균을 적용한 결과입니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
SCRIPT({
    const filter = require("mathx/filter")
    const { arrange } = require("mathx");
    const avg = new filter.Avg();
}, {
    for( val of arrange(1, 5, 0.03)) {
        val = Math.round(val*100)/100;
        sig = Math.sin( 1.2*2*Math.PI*val );
        noise = 0.09 * Math.cos(9*2*Math.PI*val) + 
                0.15 * Math.sin(12*2*Math.PI*val);
        $.yield( val, sig + noise, avg.eval(sig+noise) );
    }
})
CHART(
    size("600px", "400px"),
    chartOption({
        xAxis:{ type: "category", data: column(0)},
        yAxis:{ max:1.5, min:-1.5 },
        series:[
            { type: "line", data: column(1), name:"value+noise" },
            { type: "line", data: column(2), name:"AVG" },
        ],
        legend: { bottom: 10 },
    })
)

FAKE(arrange(1,5,0.03))
MAPVALUE(0, round(value(0)*100)/100)
SET(sig, sin(1.2*2*PI*value(0)) )
SET(noise, 0.09*cos(9*2*PI*value(0)) + 0.15*sin(12*2*PI*value(0)))
MOVAVG( value(1), window(10) )
CHART(
    size("600px", "400px"),
    chartOption({
        xAxis:{ type: "category", data: column(0)},
        yAxis:{ max:1.5, min:-1.5 },
        series:[
            { type: "line", data: column(1), name:"value+noise" },
            { type: "line", data: column(2), name:"avg" },
        ],
        legend: { bottom: 10 }
    })
)

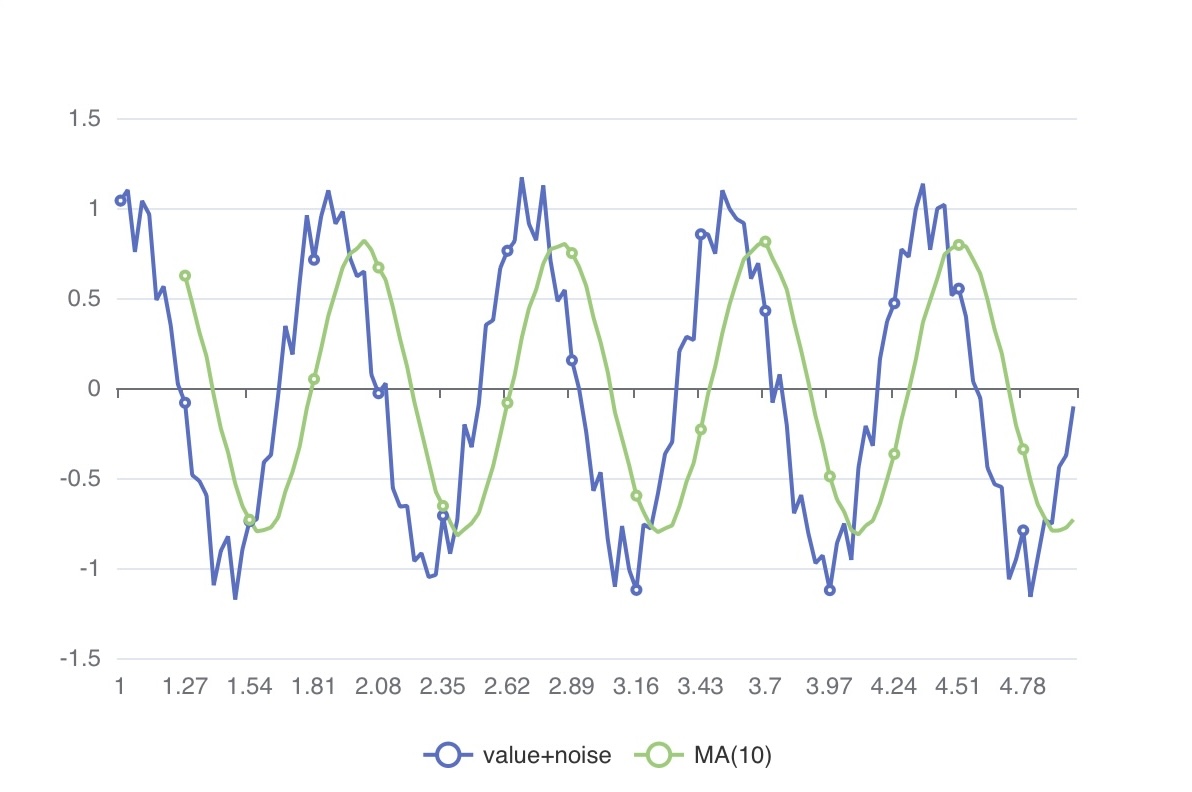
이동 평균

누적된 전체 샘플에 대해 평균을 계산하는 대신, 고정된 크기의 샘플 구간(window)을 사용해 평균을 계산합니다. 이는 주식 차트에서 흔히 보는 n일 이동 평균과 같은 개념입니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
SCRIPT({
    const { arrange } = require("mathx");
    const filter = require("mathx/filter")
    const movavg = new filter.MovAvg(10);
    $.result = { columns: ["val", "sig", "ma10"], types: ["double", "double", "double"] }
}, {
    for( val of arrange(1, 5, 0.03)) {
        val = Math.round(val*100)/100;
        sig = Math.sin( 1.2*2*Math.PI*val );
        noise = 0.09 * Math.cos(9*2*Math.PI*val) + 
                0.15 * Math.sin(12*2*Math.PI*val);
        $.yield( val, sig + noise, movavg.eval(sig+noise) );
    }
})
CHART(
    size("600px", "400px"),
    chartOption({
        xAxis:{ type: "category", data: column(0)},
        yAxis:{ max:1.5, min:-1.5 },
        series:[
            { type: "line", data: column(1), name:"value+noise" },
            { type: "line", data: column(2), name:"MA(10)" },
        ],
        legend: { bottom: 10 },
    })
)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
FAKE(arrange(1,5,0.03))
MAPVALUE(0, round(value(0)*100)/100)
SET(sig, sin(1.2*2*PI*value(0)) )
SET(noise, 0.09*cos(9*2*PI*value(0)) + 0.15*sin(12*2*PI*value(0)))
MAPVALUE(1, $sig + $noise)
MAP_MOVAVG(2, value(1), 10)
CHART(
    size("600px", "400px"),
    chartOption({
        xAxis:{ type: "category", data: column(0)},
        yAxis:{ max:1.5, min:-1.5 },
        series:[
            { type: "line", data: column(1), name:"value+noise" },
            { type: "line", data: column(2), name:"MA(10)" },
        ],
        legend: { bottom: 10 }
    })
)

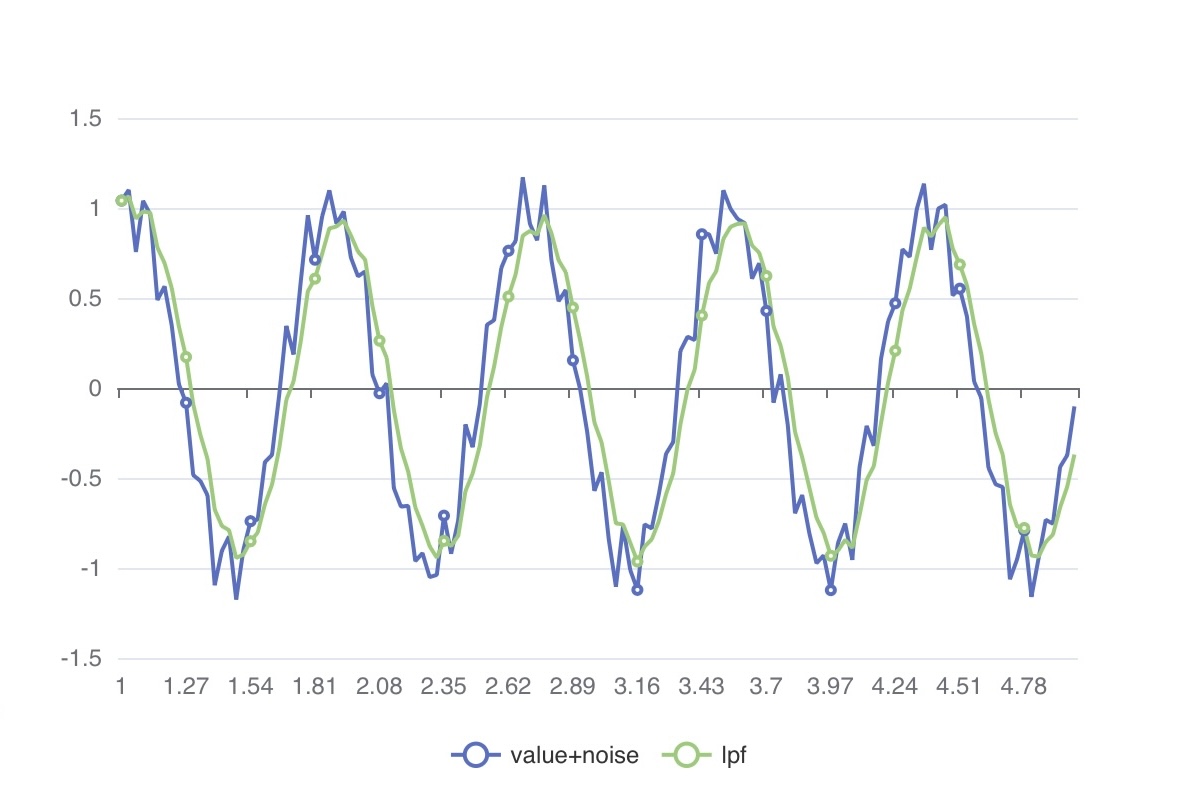
저역 통과 필터

이동 평균은 사용하기 쉽고 이해하기도 쉽지만, 몇 가지 한계가 있습니다.

윈도우 안의 모든 샘플에 동일한 가중치를 적용하므로 최근 추세를 반영하는 속도가 느릴 수 있습니다. 또한 값이 크게 변하는 구간에 비교적 둔감합니다. 이를 보완하기 위해 평균을 계산할 때는 윈도우 안의 최근 값과 오래된 값에 서로 다른 가중치를 주는 방식을 흔히 사용합니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
SCRIPT({
    const { arrange } = require("mathx");
    const filter = require("mathx/filter")
    const lowpass = new filter.Lowpass(0.40);
    $.result = { columns: ["val", "sig", "lpf"], types: ["double", "double", "double"] }
}, {
    for( val of arrange(1, 5, 0.03)) {
        val = Math.round(val*100)/100;
        sig = Math.sin( 1.2*2*Math.PI*val );
        noise = 0.09 * Math.cos(9*2*Math.PI*val) + 
                0.15 * Math.sin(12*2*Math.PI*val);
        $.yield( val, sig + noise, lowpass.eval(sig+noise) );
    }
})
CHART(
    size("600px", "400px"),
    chartOption({
        xAxis:{ type: "category", data: column(0)},
        yAxis:{ max:1.5, min:-1.5 },
        series:[
            { type: "line", data: column(1), name:"value+noise" },
            { type: "line", data: column(2), name:"lpf" },
        ],
        legend: { bottom: 10 },
    })
)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
FAKE(arrange(1,5,0.03))
MAPVALUE(0, round(value(0)*100)/100)
SET(sig, sin(1.2*2*PI*value(0)) )
SET(noise, 0.09*cos(9*2*PI*value(0)) + 0.15*sin(12*2*PI*value(0)))
MAPVALUE(1, $sig + $noise)
MAP_LOWPASS(2, $sig + $noise, 0.40)
CHART(
    size("600px", "400px"),
    chartOption({
        xAxis:{ type: "category", data: column(0)},
        yAxis:{ max:1.5, min:-1.5 },
        series:[
            { type: "line", data: column(1), name:"value+noise" },
            { type: "line", data: column(2), name:"lpf" },
        ],
        legend: { bottom: 10 }
    })
)

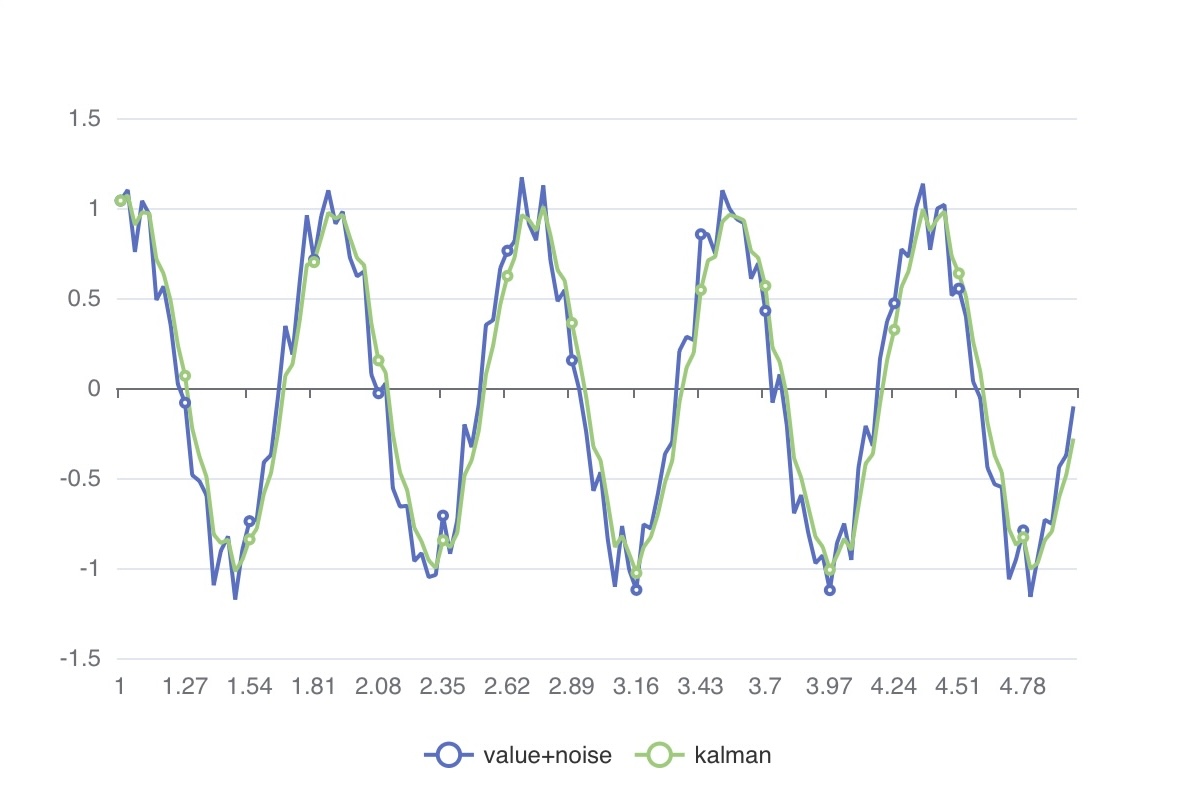
칼만 필터

MAP_KALMAN() 함수의 model() 인자는 수학적 시스템 변수를 나타내는 입력값을 받습니다. 최적의 시스템 값을 어떻게 정할지는 이 문서의 범위를 벗어납니다. 다만 실제로는 TQL에서 간단한 칼만 필터 모델을 쉽게 적용해 보고, 경험적으로 최적의 파라미터를 반복적으로 찾아갈 수 있습니다.

아래 예제는 model 값의 변화가 그래프에 어떤 영향을 주는지 보여줍니다. 여러 model 값을 적용해 보면서 그래프가 어떻게 반응하는지 확인해 보실 수 있습니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
SCRIPT({
    const { arrange } = require("mathx");
    const filter = require("mathx/filter")
    const kalman = new filter.Kalman(0.1, 0.5, 1.0);
    $.result = { columns: ["val", "sig", "kalman"], types: ["double", "double", "double"] }
}, {
    for( val of arrange(1, 5, 0.03)) {
        val = Math.round(val*100)/100;
        sig = Math.sin( 1.2*2*Math.PI*val );
        noise = 0.09 * Math.cos(9*2*Math.PI*val) + 
                0.15 * Math.sin(12*2*Math.PI*val);
        $.yield( val, sig+noise, kalman.eval(new Date(), sig+noise) );
    }
})
CHART(
    size("600px", "400px"),
    chartOption({
        xAxis:{ type: "category", data: column(0)},
        yAxis:{ max:1.5, min:-1.5 },
        series:[
            { type: "line", data: column(1), name:"value+noise" },
            { type: "line", data: column(2), name:"kalman" },
        ],
        legend: { bottom: 10 },
    })
)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
FAKE(arrange(1,5,0.03))
MAPVALUE(0, round(value(0)*100)/100)
SET(sig, sin(1.2*2*PI*value(0)) )
SET(noise, 0.09*cos(9*2*PI*value(0)) + 0.15*sin(12*2*PI*value(0)))
MAPVALUE(1, $sig + $noise)
MAP_KALMAN(2, $sig + $noise, model(0.1, 0.6, 1.0))
CHART(
    size("600px", "400px"),
    chartOption({
        xAxis:{ type: "category", data: column(0)},
        yAxis:{ max:1.5, min:-1.5 },
        series:[
            { type: "line", data: column(1), name:"value+noise" },
            { type: "line", data: column(2), name:"kalman" },
        ],
        legend: { bottom: 10 }
    })
)

최근 업데이트 Mar 9, 2026

FFT()시간 관련 예제